Animating images in Java (2)

Moving images on the screen, following a target

In previous part we have animated images in place — changed their appearance. In this part we will make them move. The source code is at demo006.

First, a little more math

Moving an image is fundamentally the same process as changing its appearance, only instead of changing which bitmap is displayed depending on time, we change the coordinates it is displayed at.

(We can also change both. A running figure will simultaneously changes its shape and its position. Let’s focus on the position now.)

The easiest way would be to make a coordinate depend on time. We keep the system from the previous part: a “javax.swing.Timer” that redraws the screen in regular intervals, and a “totalTime” variable that tracks how many milliseconds have passed.

int x = totalTime;
g.drawImage(myImage, x, 0, null);

Yes, this would move the image… very fast to the right; and then it flies away from the screen and disappears. So we have two problems here: how to slow down the motion, and how to keep the image within the screen.

Why did the image move so fast in the first place? Consider the units:

• variable “totalTime” measures the time in milliseconds

• variable “x” specifies the horizontal position in pixels

Assigning “x = totalTime” implies¹ the conversion rate of 1 pixel per millisecond; that is 1000 pixels per second. That is a fast movement.

Suppose we want the image to move e.g. 20 pixels per second. We can do it like this:

int x = totalTime * 20 / 1000;

It is important to do the multiplication before the division. If instead we assigned “x = totalTime / 1000 * 20”, it would make the image jump by 20 pixels each second instead of moving fluently. That’s because integer division rounds down the results. (We need to round the final result, but not the intermediate results.)

We could exploit the fact that 20 is a divisor of 1000, and write “x = totalTime / 50”.

Or we could use floating-point numbers instead of integers and then we don’t have to worry about the order of operations. Like this:

float timeInSeconds = totalTime / 1000.0f;
float x = 20 * timeInSeconds;
g.drawImage(myImage, Math.round(x), 0, null);

To prevent the image from disappearing off the right side of the screen, we could limit the x coordinate to a certain interval. To keep x between zero and 400 we can write:

x = (totalTime * 20 / 1000) % 400;

Now the values of x are limited to minimum 0 and maximum 399. Notice that we slow down first (in parentheses, or on a previous line of code), and set the limit later.

The image now moves slowly to the right… and then teleports back to the beginning. Cool if that’s what we wanted. But maybe we wanted it to bounce off the right edge and return fluently to the beginning; and then bounce again, etc.

To achieve that, we need to use the length of the entire cycle (in this case, 800 pixels) using the “%” operator, and then adjust the result. Like this:

int x = (totalTime * 20 / 1000) % 800;
if (x > 400) {
    x = 800 - x;
}

Or maybe like this; that’s just another way to express the same idea:

int phase = (totalTime * 20 / 1000) % 800;
int x = (phase < 400) ? phase : (800 - phase);

More abstractly:

int phase = (totalTime * SPEED / 1000) % (2 * DISTANCE);
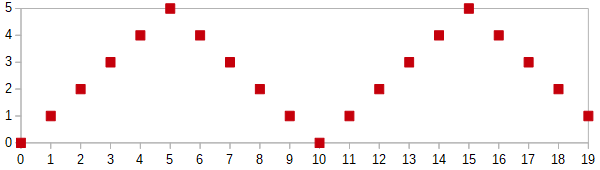
int x = (phase < DISTANCE) ? phase : (2 * DISTANCE - phase);

That creates a bouncing motion: during the first half of the cycle the image moves to the right, during the second half of the cycle it moves to the left.²

Graph of “(p < 5) ? p : (10 - p)” where “p = t % 10”

But maybe we don’t want the image to bounce off an invisible wall, and instead want it to speed up and slow down gradually. So that not only the position of the image, but also its speed changes fluently.

There is actually a mathematical formula ready for that, in trigonometry. Actually a pair of functions called sine and cosine. Without going into too much detail now, let’s just say that they are a more fluent version of the bouncing graph above. Their values are floating-point numbers between -1.0 and 1.0, and the length of the cycle is 2π, which is about six and a quarter.

(We do not use the “%” operator anymore, because the cycle is already built in.)

double timeInSeconds = totalTime / 1000.0;
double x = 200 + 200 * Math.sin(timeInSeconds);
g.drawImage(myImage, (int) Math.round(x), 0, null);

The implementation of “Math.sin” in Java uses “double”; “Math.round” converts “double” to “long”; but the function “drawImage” requires “int”… so we need to put an implicit type cast somewhere — either “double” to “float”, or “long” to “int”.

Notice that sine and cosine also return negative values, so “200 + 200 * …” prevents the image from leaving the left side of the screen, by setting the range from 0 to 400.

The length of the cycle is about 6.28 seconds. If we want to change it to a specific value, for example N seconds, we need to do the following:

double x = CENTER + RADIUS * Math.sin(timeInSeconds * N / (2 * Math.PI));

Some examples are in MovingAnimationView.

The flying saucer bounces horizontally, the colored balls move smoothly vertically

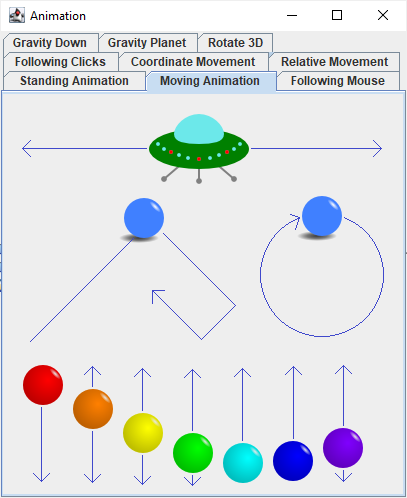
The flying saucer does the bouncing movement, using the “%” operator.

The colored balls at the bottom do the fluent movement, using the “Math.sin” function. They move vertically, because their y coordinate changes rather than x. They move in a wave-like composition (the red one first, followed by the orange one, etc.), because the argument for the “Math.sin” function is adjusted by a small constant (a different constant for each ball) making their movement slightly delayed in time.

Finally, there are two blue balls that move in both directions. The ball on the left uses the bouncing movement for both its x and y coordinates. Because each coordinate bounces independently and with a different cycle length, it creates an impression of a ball bouncing inside an invisible box.

The ball on the right uses “Math.sin” for one of its coordinates, and “Math.cos” for the other. Together these two functions create a circular motion. (You could create an elliptical motion by multiplying the coordinates by different numbers. You could create a weird fluent motion by giving them different cycle lengths.)

Then, a little physics… I mean, more math again

In previous examples (both changing the image and changing the coordinates), the animation was predetermined, like a movie. Let’s make it interactive instead.

The concept of “total time” is no longer useful. Even if we know how much time has passed since the beginning of the animation, the position of the object depends on whatever happened during that time.

We don’t even need to remember the entire history. We just have to remember the last state, and update it depending on how much time has passed since then. (Which is the same concept as updating the game state in the incremental game. “Passing of time is just another kind of event.”)

What is the “state” here? All things that change, and therefore we need to remember them. At the very least, the positions of the objects, and if we want them to have some kind of inertia, also their speeds.

In a two-dimensional space, such as on the computer screen, the position of an object is specified by two numbers: its coordinates x and y. (If it rotates, also the angle.)

The speed of an object is also specified by two numbers, but their meaning is different — in physics, they would have different units — its speed along the x-axis, and its speed along the y-axis. (If it rotates at variable speeds, also the speed of rotation.)

Because we will use pairs of numbers quite often, it makes sense to encapsulate them as a single object. We can use an existing class, such as “Point2D.Double” from the AWT library, or create a new one, such as Vector2D in the example project.

In physics, uniform rectilinear motion would be described as:

\(v = \frac{\Delta x}{\Delta t}\)

which can translate to Java like this:

position.x += speed.x * timePassed;
position.y += speed.y * timePassed;

or, using objects, like this:

position = position.add(speed.multiply(timePassed));

In simple calculations, most of the time, the calculations involve doing the same thing twice, once with the x coordinate, and once with the y coordinate. A notable exception is calculating the length of the vector. (If the vector represents speed, calculating its length means finding out the total speed, from its partial speeds along the x and y axes.) Using the Pythagorean theorem:

length = Math.sqrt(x * x + y * y);

Let’s see an example in MouseFollowingView.

The flying saucer follows the cursor like its shadow, the balls move fluently

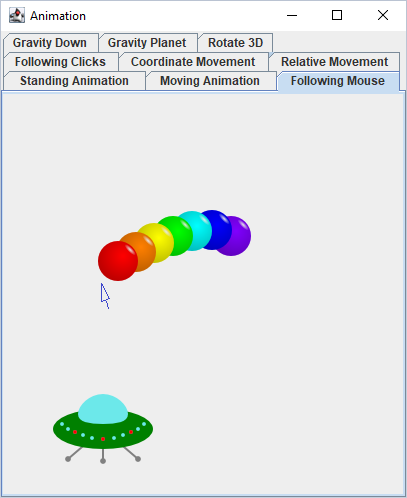
The flying saucer updates its x coordinate immediately to match the position of the mouse cursor. Its y coordinate remains constant. For this kind of moving object we do not need to remember any state, as it does not depend on history at all.

The colored balls move gradually towards their targets, therefore we need to remember their positions. But they move at a constant speed and have no inertia, therefore we do not need to remember their speeds.

The red ball follows the mouse cursor, the orange ball follows the red ball, etc. Together this creates a kind of caterpillar, crawling towards the cursor.

First, the direction towards the target is determined. I will write the algorithm here using separate variables, but in actual code the behavior is encapsulated in objects.

distanceX = targetX - positionX;
distanceY = targetY - positionY;

Then we calculate the distance from the target:

distance = Math.sqrt(distanceX * distanceX + distanceY * distanceY);

Then we calculate how far we can actually move at the speed of 100 pixels per second:

maxDistance = 100 * timeInMilliseconds / 1000;

We do not want to move entirely to the top of the target, but to stop at a 20-pixel distance. So the actual distance moved would be the distance to target minus 20, but not more than the distance permitted by the speed limit, and not less than zero.

movement = Math.max(0.0, Math.min(distance - 20, maxDistance));

From this we can calculate the x and y distances to move. Beware the division by zero!

moveX = (0.0 == movement) ? 0.0 : (distanceX / distance * movement);
moveY = (0.0 == movement) ? 0.0 : (distanceY / distance * movement);

And finally, we move the object:

positionX += moveX;
positionY += moveY;

As you can see, hiding the two coordinates in a class reduces a lot of repetition.

To avoid possible bugs, I recommend using immutable objects. That is, instead of updating the x and y values (of either the position or the distance), create a new object.

A more game-like example

In an actual game, we would have multiple moving objects, each doing their own behavior. The player could select some of those objects and give them commands.

With the knowledge we already have, doing something like that is simple. We only need a few more concepts:

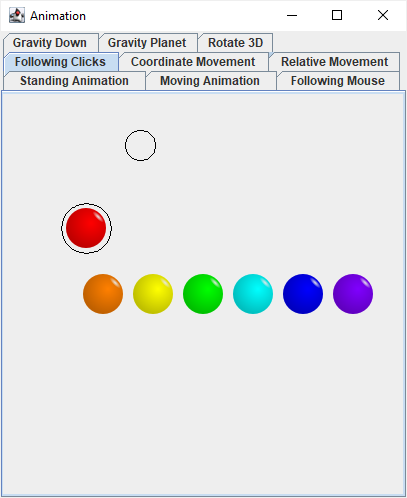
• Each ball remembers its target position. At the beginning of the “game”, the target position is the same as the starting position, i.e. the balls do not move initially. When the target position is not the same as the current position, the ball moves towards it.

• We remember which ball is currently selected.

• The player can select a ball by clicking on it. Clicking on a moving ball can be more difficult for the player than clicking on a stationary one, but it makes no difference to the algorithm: it means clicking sufficiently close to the ball’s (current) position. After clicking, we check all balls in a loop.

• Right-clicking sets the target for the selected ball. It just sets a variable.

• We update the painting method to also display the selection and the targets.

This is implemented in ClickFollowingView. With a lot of imagination it resembles selecting and moving units in real-time strategies such as the old Warcraft games.

Left-click to select a ball, right-click to set its destination

By the way, in the last two examples, the “position” variable of a ball represents its center, i.e. not the upper-left corner, as the “drawImage” method would expect.

This requires extra adjustment when calling the “drawImage” method, but it makes the calculations (distance of a point from the ball) easier.

Even when you have non-spherical moving objects, it is worth considering that choosing their coordinates to be something other than the upper-left corner could make the calculations more natural.

1. We could avoid this kind of implied conversion by creating separate data types for tracking time, and for tracking positions. If we had different data types for different units, carelessly assigning “x = t” would cause a compile-time error; a reminder to set up the conversion rate.

2. Some nitpicking: The previous equation “t % 400” provided values between 0 and 399. The new equation “(p < 400) ? p : (800 - p) where p = t % 800” returns values between 0 and 400.

Is this okay? Or would you prefer if the equation returned values between 0 and 399 in the first half of the cycle, and then values from 399 down to 0 in the second half? That is, return the values 0 and 399 twice, but never exceed 399? If that is what you want, then the equation becomes “(p < 400) ? p : (800 - 1 - p) where p = t % 800”. Notice the “minus one” part.