Animating images in Java (3)
Flying in 2D, gravity, rotations in 3D
In previous part, we learned how to move images on the screen — change their coordinates in response to the passage of time, and to user’s actions.
Interactive animations require us to remember state. In the example with selecting and moving colored balls across the screen, the state consisted of:
the current position of each ball
the target of each ball
which ball is currently selected
(Notice that the state is a list of variables you have to declare.)
Today, let’s try more complicated states.
Inertia
Newton’s first law of motion says: “Every object perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.”
Let’s implement this in Java.
In addition to the position of the object, we also need to remember its speed. User can change the speed (in this case, by pressing arrow keys on the keyboard), but the default behavior is that the speed remains the same unless something happens, and the position updates according to the speed and the time passed.
positionX += time * speedX;
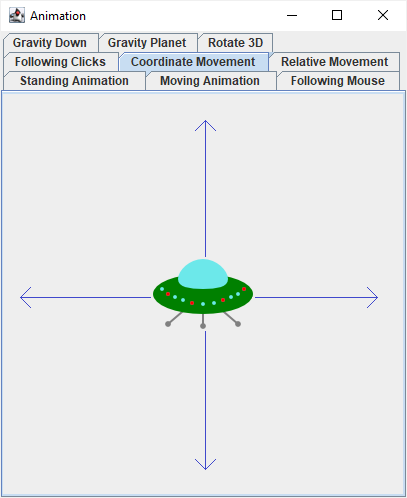
positionY += time * speedY;This is the main idea behind CoordinateMovingView; the rest are technical details.
At the beginning, variables “speedX” and “speedY” are set to zero; the saucer stands.
Pressing one of the four arrow keys set the variables accordingly. Moving left or right sets “speedX” to -1 or 1 respectively, and “speedY” to zero. Moving up or down sets “speedY” to -1 or 1 respectively, and “speedX” to zero. (The flying saucer changes its position fluently based on its speed; but it changes its speed abruptly.)
After updating the position based on the speed, further checks are applied to prevent the flying saucer from leaving the window. If the x coordinate is too low or too high, it is set to the minimum or maximum value respectively. Same with the y coordinate.1
Also, this animation combines changing the coordinates and changing the shape, i.e. the previous two lessons. The motion of the flying saucer depends on the keys pressed. But the lights on the saucer keep blinking depending on the total time.
Rotation
If we want to move an object in an oblique direction, we can achieve it by setting both “speedX” and “speedY” to nonzero values.
But sometimes we also want the object to be facing a certain direction. Even if it is not moving at the moment, or if it happens to be moving (e.g. by inertia) in a different direction. This is often used in top-view games.
We could allow only a certain selection of angles, such as multiples of 90° or 45° or 15°, or we could allow an arbitrary angle.
Now we have to calculate what it means to move in a certain direction. If the object is facing a certain direction, what does it mean for the object to take a step forward? How will the x and y components of its position change?
If we only allow multiples of 90°, it is easy. This is a less elegant, but very obvious way to write the code:
int direction = ...; // 0 = up, 1 = right, 2 = down, 3 = left
if (0 == direction) {
positionY -= distance;
} else if (1 == direction) {
positionX += distance;
} else if (2 == direction) {
positionY += distance;
} else {
positionX -= distance;
}Instead of branching the code, we could extract the x and y components of each direction to constant arrays, and write the code like this:
int[] X_COMPONENTS = { 0, 1, 0, -1};
int[] Y_COMPONENTS = {-1, 0, 1, 0};
int direction = ...;
positionX += X_COMPONENTS[direction] * distance;
positionY += Y_COMPONENTS[direction] * distance;If we allow multiples of 45°, the second approach scales better. We need to add a few constants for the new directions. However, we need to start using floating-point numbers, because moving 1 pixel diagonally means moving √½ pixels along each axis.
double S = Math.sqrt(0.5);
double[] X_COMPONENTS = { 0.0, S, 1.0, S, 0.0, -S, -1.0, -S};
double[] Y_COMPONENTS = {-1.0, -S, 0.0, S, 1.0, S, 0.0, -S};
int direction = ...; // 0 = up, 1 = up-right, 2 = right...
positionX += X_COMPONENTS[direction] * distance;
positionY += Y_COMPONENTS[direction] * distance;We could use a math textbook to find the values for multiples of 15°. But it would probably be easier to use the general formula instead:
double directionInRadians = ...; // 0.0 = up, then clockwise
positionX += Math.sin(directionInRadians) * distance;
positionY -= Math.cos(directionInRadians) * distance;(Notice the minus in the last line. That’s because “Math.cos” starts with 1, but moving upwards decreases the y coordinate. Alternatively, we could decide that the angle 0.0 means downwards. Don’t forget to document your code to make this clear.)
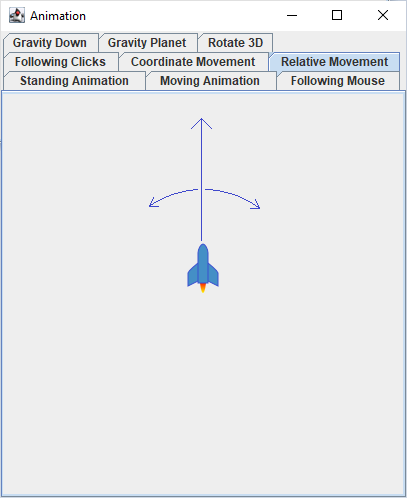
The example in RelativeMovingView uses multiples of 45°. The rocket moves at a constant speed, but pressing an arrow key left or right changes its direction. If the rocket leaves the screen, it reappears at the opposite edge.
Pressing the space key shoots missiles, which move the same way as the rocket, only faster. They disappear when they leave the screen.
To implement the position and rotation, we use a helper class “PositionAndTurn”. Values “x” and “y” are floating-point, “turn” is an integer between 0 and 7. (This class is inspired by turtle graphics.) Once we have encapsulated the position and angle of an object in a separate class, the rest of the program becomes very simple:
moving left or right means changing the rocket’s angle
shooting a missile means creating a new missile at the rocket’s position and angle
both the rocket and the missiles move forward, each at its own speed
check if the rocket or a missile left the screen
draw the rocket using the image that corresponds to its angle
That’s it.
The last point would become more of a problem if we tried to implement a rocket that can turn at an arbitrary angle. We cannot have an unlimited number of bitmaps, and rotating a bitmap on the fly would be too difficult. (Probably also slow.)
A practical solution would be to have a certain number of images, for example 24 images at 15°, and choose the one that is closest to the actual angle.
Acceleration
Newton’s second law of motion says: “The change of motion of an object is proportional to the force impressed; and is made in the direction of the straight line in which the force is impressed.”
So far, we haven’t actually considered forces. Even inertia only applied until we pressed a key, and then it magically disappeared. This is not how it works in real life.
It would be very easy to change the flying saucer code in a way that allows it to accelerate and decelerate. Instead of:
if (KeyEvent.VK_RIGHT == keyCode) {
speedX = 1;
speedY = 0;
}simply write:
if (KeyEvent.VK_RIGHT == keyCode) {
speedX++;
}Do not set the speed to a new value; instead, modify the existing value.
Now pressing an arrow key will make the standing object move, and pressing the same key again will make it move twice as fast. Pressing the opposite arrow key will slow it down to 1× speed, and pressing the opposite key again will make it stop.
Also, pressing two perpendicular arrow keys will make the object move diagonally.
Notice that the speed in this example is still quantized — proportional to how many times each button was pressed, as opposed to how long it was kept pressed. That’s because if we make the change in speed proportional to how long the button was pressed, it will become practically impossible to stop an object (to set its speed exactly to 0.0) once it starts moving… unless we also introduce the concept of friction.
Gravity
To implement gravity, we need to use the kind of acceleration that applies over time. Gravity not only allows things to fall down; it also allows jumping, otherwise each jump would send us flying away to space.
In physics, acceleration is defined as:
Seems familiar? Acceleration is to speed like speed is to distance. Even in Java:
speed.x += acceleration.x * timePassed;
speed.y += acceleration.y * timePassed;is similar to:
position.x += speed.x * timePassed;
position.y += speed.y * timePassed;To make objects accelerate — and to make them fall down due to gravitational acceleration — requires us to include both sets of commands in code.
But… which one should go first?
This question does not make sense in physics. Both of these changes keep happening continuously, in parallel. Dealing with non-infinitesimal slices of time is a specific problem of programming.
We could update the position using the old value of speed, and then update the speed. Or we could update the speed first, and then update the position using the new value. Perhaps it would be best to use the average of the old and the new speed.2
But before we needlessly complicate our code, let’s crunch some numbers and see how much of a difference it makes.
Imagine an object that starts motionless, and then accelerates at 1 m/s². According to physics, during the first second, the object should move 0.5 meters away.
Suppose we only make one update, using the time interval of 1 second. If we update the position first, the object will not move at all (because the starting speed is zero). And then we update the speed, but it is too late to matter.
If we instead update the speed first, it becomes 1 (acceleration × time = 1×1), and then we update the position, and it also becomes 1 (speed × time = 1×1). So depending on the order of the updates in code, the object will move either 0 or 1 meter.
Suppose we make two updates, each using time interval of 0.5 seconds. First option is that the speed remains zero (speed × time = 0×0.5), then the speed becomes 0.5 (acceleration × time = 1×0.5), then the position becomes 0.25 (speed × time = 0.5×0.5), and finally the speed becomes 1 (previous speed + acceleration × time = 0.5+1×0.5).
If we do it the other way round, first the speed becomes 0.5, then the position becomes 0.25 (speed × time = 0.5×0.5), then the speed becomes 1, and finally the position becomes 0.75 (previous position + speed × time = 0.25+1×0.5).
When the updates are more frequent and smaller, the precision increases. For one update, it is 0 versus 1, for two updates, it is 0.25 versus 0.75. For more updates:
number of updates | 1 | 2 | 3 | 4 | 10 | 20
update position first | 0.0 | 0.25 | 0.333 | 0.375 | 0.45 | 0.475
update speed first | 1.0 | 0.75 | 0.667 | 0.623 | 0.55 | 0.525With twenty or more updates per second, the error is probably negligible. We are not talking about actual rockets here, right? It’s just a game: run it, and if it feels okay, then it is okay. (Or use the average speed.)
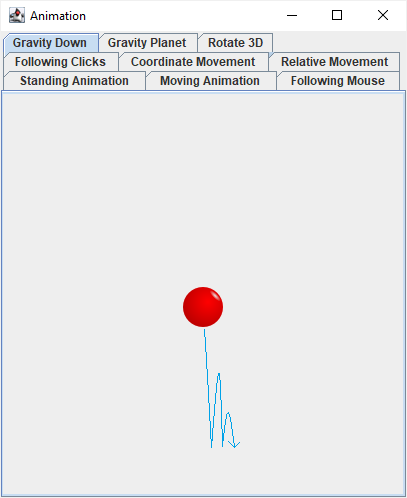
Example in GravityDownView demonstrates gravity and friction.
The ball falls down due to gravity. Clicking the screen kicks the ball in that direction.
Gravitational acceleration is downwards, 200 pixels per second per second. How did I find that value? I simply tried various values, until I found one that felt right.
I don’t know what is the proper formula for friction in physics. (Probably something complicated.) I implemented friction as a “tax on speed”, 10% per second. Again, 10% because I tried various values and that one felt right.
The entire algorithm for speed, gravitational acceleration, and friction, is like this:
float GRAVITY = 200.0f;
float FRICTION = 0.1f;
float time = timeInMilliseconds / 1000.0f;
position.x += time * speed.x;
position.y += time * speed.y;
speed.y += time * GRAVITY;
speed.x *= 1 - (time * FRICTION);
speed.y *= 1 - (time * FRICTION);Also, the ball bounces at the ends of the screen. We need to flip both the position and the speed:
if (position.x < MIN_X) {
position.x = 2 * MIN_X - position.x;
speed.x = Math.abs(speed.x);
}
if (position.x > MAX_X) {
position.x = 2 * MAX_X - position.x;
speed.x = -Math.abs(speed.x);
}
if (position.y < MIN_Y) {
position.y = 2 * MIN_Y - position.y;
speed.y = Math.abs(speed.y);
}
if (position.y > MAX_Y) {
position.y = 2 * MAX_Y - position.y;
speed.y = -Math.abs(speed.y);
}Gravity in space
Constant gravitational acceleration downwards is good for everyday situations on the surface of Earth (or some other planet), but what if we want to fly in space?
The general formula for gravitational force in space is:
(where G is a gravitational constant, and r is a distance between two bodies), and the formula for acceleration is:
Putting these equations together, m₁ reduces and we get:
In practice, gravity of things smaller than planets or moons is negligible. So if we have e.g. two battleships fighting among the planets, we only need to calculate how much they are attracted to the planets, and we can ignore the the attraction between the battleship. (We can also ignore how much the planets are attracted to the battleships.)
We need to calculate the distance between the rocket and the planet:
distance.x = planet.x - rocket.x;
distance.y = planet.y - rocket.y;
totalDistance = Math.sqrt(distance.x * distance.x + distance.y * distance.y);If we are going to make up the values of G and m₂ anyway, and try what feels right, we may simply make up their product, and the whole equation reduces to:
totalAcceleration = PLANET_CONSTANT / (totalDistance * totalDistance);and then we need to point that acceleration towards the planet:
acceleration.x = totalAcceleration * distance.x / totalDistance;
acceleration.y = totalAcceleration * distance.y / totalDistance;If there are multiple planets, we calculate the acceleration towards each of them individually, and sum up the individual results.
And then it’s the usual:
speed.x += time * acceleration.x;
speed.y += time * acceleration.y;
position.x += time * speed.x;
position.y += time * speed.y;By the way, planets are large. When we talk about a distance from the planet, we actually mean the distance from the center of the planet. And the distance needs to be larger than the radius of the planet, otherwise the rocket has already crashed on it.3
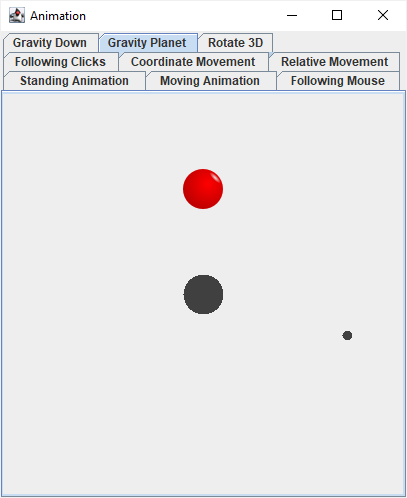
Example in GravityPlanetView demonstrates gravity in space.
The planet is in the center. The moon orbits around it, using the simple circular motion from the first part.
The ball is attracted to both bodies, but the planet is 4× heavier than the moon. Left mouse button teleports the ball; right mouse button kicks it towards the mouse cursor.
Three dimensions
To move objects in three dimensions instead of two, we need coordinates x, y, and z.
Then we need to decide how to display them on the two-dimensional computer screen. This is an independent decision: imagine moving objects in a virtual space, and then positioning a camera to get the best shot.
The easiest way is to make the space-x same as the screen-x, the space-y same as the screen-y, and ignore the space-z except for visibility: if two objects have the same screen-x and screen-y, the space-z decides which one of them is visible.
(There are also other options available, such as cabinet projection, isometric projection, or perspective. All of them display the same 3D object, but use a different strategy to translate the x, y, z of space to the x, y of the screen. When using perspective, we also need to change the size of the image depending on its distance.)
To make an actual 3D game, it would be best to use a specialized library. I am not interested in studying specific libraries, so this example will be relatively simple. We will avoid all the complexity involved in drawing polygons by only animating a few balls in space. The advantage of a ball is that it looks exactly the same from each angle.
The balls will rotate around the center.
Rotations in the three-dimensional space are calculated by Matrix3D. In mathematics, a matrix is basically a table that specifies how much individual values in the rows transform into individual values in the columns. In case of 3D coordinates, how much of the original x, y, and z coordinates turns into the new x, y, and z coordinates.
We use the sine and cosine functions again. The cosine specifies how much of the rotated coordinate remains, and the sine specifies how much of it becomes the other coordinate. (We only do rotations around one of the three axes, not the oblique ones.)
Class Rotate3DView implements the example. There are two shapes constructed out of small balls: cube and octagon. You can switch them using the “C” and “O” keys.
Arrow keys rotate the structure: up and down, left and right, Page Up and Page Down; each pair rotates around a different axis. And other key pauses the rotation.
To improve the illusion of three dimensions, the balls “far behind the screen” are pale.
To draw the balls in the correct order we first collect their images along with their positions in a helper class “ImageToPaint”, sort it by distance from the screen, and then draw them starting with the ones in the back, and proceeding to the front.
And that’s enough theory about animations. Try to make some nice ones yourself.
This prevents the saucer from leaving the allowed coordinate range, although in some sense it keeps trying, because the values “speedX” and “speedY” did not change; they keep pointing outside the allowed range. Would it be better to also set them to zero?
As the program is now, it wouldn’t make a change from the user’s perspective. But there are situations where it could. For example, if the allowed range of positions changed as a result of something happening in the game, e.g. a door opens, and a previously stuck object can pass through. Or if the shape of the image depended on its speed, for example a figure could either stop next to the wall, or keep pushing against it.
That is indeed the correct answer, assuming that the acceleration itself remains constant. But if the acceleration changes, we would need to use calculus to figure out the correct formula.
Even if the rocket wouldn’t crash on the planet — that is, if the planet had a tunnel that the rocket could fly through — the formula would no longer work when the rocket is below the surface of the planet.
Below the surface, the gravitational force decreases — linearly, if we assume a homogeneous spherical planet — and becomes zero at its center. (As opposed to the original formula, which would give us infinity — division by zero — at the center.)